Square Root Decomposition을 사용할 때는?
검색을 할 때 빠르게 검색을 하기 위해 구간을 나눈 후 찾을 때 많이 사용된다. 사실 Segment Tree를 사용하면 유사한 기능을 O(log N)이라는 훌륭한 시간내에 수행해낼 수 있다. 하지만 SQRT Decomposition는 Mo’s Algorithm의 기반이기에 다음을 생각하고 글을 쓴다.
sqrt decomposition이란?
주 아이디어는 연속적인 원소들을 하나의 묶음으로 생각하기이다. 값 N개를 O(√N)개의 연속된 구간들로 나누어서 관리한다. 그리고 구간에 속한 값도 O(√N)개입니다. 즉 구간 수 * 크기 = √N * √N = N이 되는 것이다. 제곱수가 아닐 경우 적당히 내림/올림을 한다.
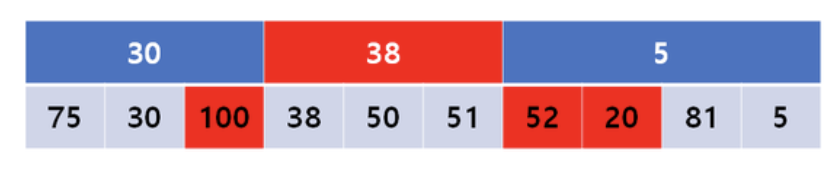
구간 내 최솟값을 구하는 것이다. 3~8번째 원소들 중 최솟값을 구하려면, 후보는 윗쪽 붉은 구간에 완벽히 포함되는 구간 노드들의 값과, 아랫쪽 붉은 구간 노드에 포함되지 못한 나머지 원소들이다. 이들 중 최소의 것을 흩어져서 찾는다.
다 하나씩 훑는데 시간이 많이 걸릴 것 같은데 꼭 그렇지 않는다. 윗쪽 붉은 구간에 해당하는 구간 노드는 최대 O(√N)개 이다. 왜냐면 애초에 구간 노드가 저만큼 밖에 없다. 아랫쪽 붉은 구간 노드에 해당하는 원소들의 개수도 O(√N)개인데, 세그먼트 트리를 분석할 때와 마찬가지로 이러한 원소들은 많아봐야 윗쪽 붉은 구간의 양 옆 구간 노드들 밖에 없다.
즉 최대 2*√N개쯤만 존재한다.
따라서 한 쿼리를 처리하는 데 O(√N)의 시간이 걸립니다.

또한 위와 같이 range가 이렇 두 구간에 포함될 때는 각 대표 구간값만 갖고 하면 된다.
sqrt decomposition update
뭔가 복잡할 것 같지만 해당 원소가 속해있는 묶음의 합에 바뀐 값의 차이만큼 더해주고 실제 원소의 값을 변경시켜주면 끝난다. 위치를 알기 때문에 시간복잡도는 O(1)이다.
time complexity
- 전처리 : O(N)
- 구간의 합을 구하는 쿼리 : O(N‾‾√)
- 특정 값을 갱신 : O(1)
http://blog.naver.com/PostView.nhn?blogId=kks227&logNo=221401154455&parentCategoryNo=311&categoryNo=&viewDate=&isShowPopularPosts=true&from=search https://kesakiyo.tistory.com/22
https://justicehui.github.io/medium-algorithm/2019/03/03/SqrtDecomposition/#:~:text=SQRT%20Decomposition%EC%9D%80%20%EC%9D%B4%EB%A6%84%20%EA%B7%B8%EB%8C%80%EB%A1%9C,(Decomposition)%ED%95%98%EB%8A%94%20%EA%B2%83%EC%9E%85%EB%8B%88%EB%8B%A4.