제 블로그의 모든 글은 IMHO로 쓴 것입니다. 잘못된 부분이 있으면 덧글을 통해서 소통을 하면 더 좋은 글로 발전이 될 수 있을 것 같습니다. 그렇지만 소통을 할 때 서로의 감정을 존중하는 선에서 해주셨으면 좋겠습니다. 감사합니다:)
그래프란?
각 점이 연결된 간선들을 저장한 것이다.
기본 용어
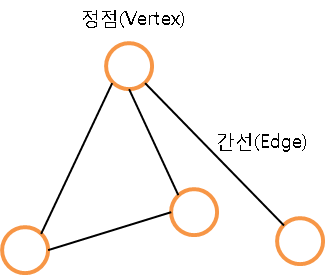
- vertex: 간선
- weight: 가중치
- 차수[degree]: 정점과 연결된 간선의 개수
- indegree: 들어오는 간선
- outdegree: 나가는 간선
- loop: 간선 양끝이 같은 것[자기에서 나와서 자기로 들어가는 것]
- cycle: 정점 A에서 다시 A로 돌아오는 경로
- path: 정점 A에서 B로 가는 경로
정점은 {1,2,3} 이렇게 표시
간선은 {(1,2), (1,5), (2,5)} 이리 표시
그래프에 있는 인접행렬과 인접리스트는 정점을 기록하는 것이 아니라,
간선을 기록하는 것이다.
예를 들어 A[1] = 2,5를 보면
1~2 연결, 1~5가 연결되어 있다.
이렇게 된 것이다.
간선을 저장하는 법
- 인접 행렬
- 인접 리스트
인접 행렬
시간,공간 복잡도 : O(V^2)
matrix = [[0] * (n+1) for i in range(n+1)]
for _ in range(m):
a, b = map(int, input().split())
matrix[a][b] = 1
matrix[b][a] = 1
인접 리스트
시간,공간 복잡도 : O(V+E)
for i in range(1,n+1):
graph[i] = set()
for _ in range(m):
a, b = map(int, input().split())
graph[a].add(b)
graph[b].add(a)
그래프 탐색
그래프 탐색에는 DFS와 BFS가 있다.
DFS는 깊이 우선 탐색이고 BFS는 넓이 우선 탐색이다.
편의를 위해
https://www.acmicpc.net/problem/1260
문제를 풀어나가며 글을 쓰겠다.
DFS[깊이 우선 탐색, Depth First Search]
루트 노드에서 시작해 그 분기를 전부 탐색 후 마지막 전의 노드들 부터 순차적으로 완벽 탐색하는 방법
[주 발상]
시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색
-> 더이상 갈 곳이 없으면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아온다.
-> 한번도 간적 없던 방향의 점점으로 탐색을 계속 반복
-> 결국 모든 정점 방문 순회
가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이우선탐색을 반복해야 하므로 후입선출 구조의 stack을 사용
DFS 그림으로 보여주기
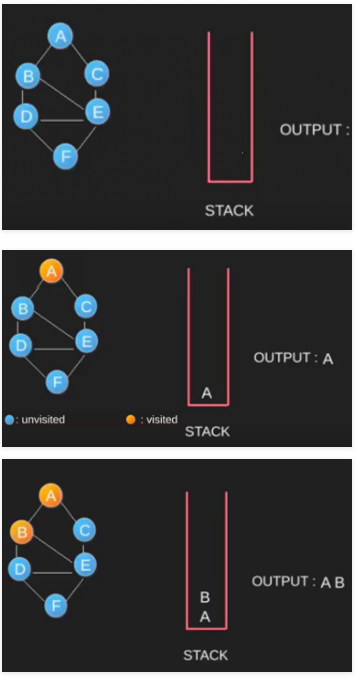
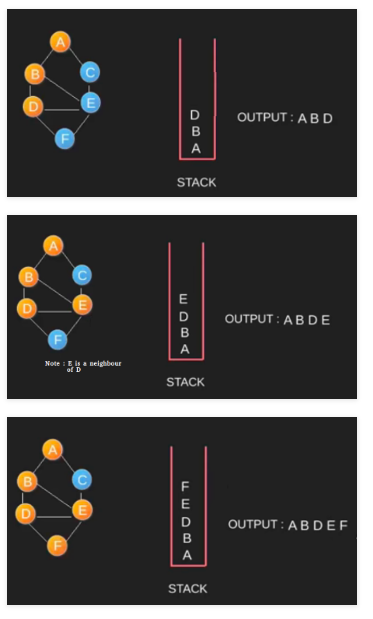
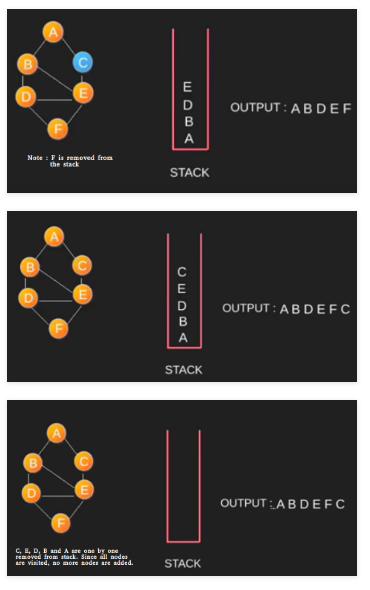
인접행렬로 풀기
input
4 5 1
1 2
1 3
1 4
2 4
3 4
n, m, v = map(int, input().split())
matrix = [[0] * (n+1) for i in range(n+1)]
for _ in range(m):
a, b = map(int, input().split())
matrix[a][b] = 1
matrix[b][a] = 1
visit=[False]*(n+1)
def dfs(i):
global visit, matrix, n
visit[i]=True
print(i, end=' ')
for j in range(n):
if matrix[i][j+1] and not visit[j+1]:
dfs(j+1)
dfs(v)
# dfs답 : 1 2 4 3
���� ��� 실제 dfs는 아니다. 원래 vertex 하나 정한 다음 방문하지 않은 인접한 vertex로 간 다음에 해당 vertex에서 다 돌면
예전 vertex에 돌아와서 전에 방문하지 않았던 인접 vertex에 인접한 것들을 방문하는 순서인데
저건 for문 돌려가지고 계속 돌다보니 다 방문하는 거다.
인접 리스트
시간,공간 복잡도 : O(V+E)
n, m, v = map(int, input().split())
graph = {}
for i in range(1,n+1):
graph[i] = set()
for _ in range(m):
a, b = map(int, input().split())
graph[a].add(b)
graph[b].add(a)
visited = [False] * (n+1)
def dfs(v):
if visited[v]:
# 만약 이미 visited한 거면 return
return 0
print(v)
visited[v] = True
for i in sorted(graph[v]):
dfs(i)
dfs(v)
# dfs답 : 1 2 4 3
인접리스트는 recursive를 이용해서 계속 새로운 depth에 일어난 일을 끝내고 바로 직전에 벌린 일을 처리 해 나간다. 마치 stack을 써서 전에 무엇을 했는지를 저장한 효과를 내는 것 처럼 말이다.
재귀를 안쓰고 stack으로 풀기
인접리스트를 쓰는게 공간복잡도 및 시간복잡도가 더 우월함으로 그걸로 개발하겠습니다.
n, m, s = map(int, input().split())
graph = {}
for i in range(1,n+1):
graph[i] = set()
for _ in range(m):
a, b = map(int, input().split())
graph[a].add(b)
graph[b].add(a)
visited = [False] * (n+1)
stack = []
stack.append(s)
while stack:
v = stack.pop()
if visited[v] :
continue
print(v, end=' ')
visited[v] = True
for u in sorted(graph[v], reverse=True):
print(u)
stack.append(u)
BFS[넓이 우선 탐색, Breadth First Search]
루트 노드에서 시작해서 인접한 노드를 탐색 한 후 순차적으로 인접 노드들의 인접 노드를 탐색하는 방법
[주 발상] 시작 정점으로부터 인접 정점을 먼저 탐색 -> 더이상 갈 곳 없으면, 가장 처음으로 갔던 인접 정점의 인접 정점들을 탐색 -> 시작 정점에서 처음으로 갔던 인접 정점의 주변부를 다 돌면 그 다음으로 갔던 인접 정점의 주변부를 탐색 -> 그렇게 순차적으로 하나씩 인접정점을 탐색 하는 행동을 반복 -> 결국 모든 정점 방문 순회
BFS 그림으로 보여주기
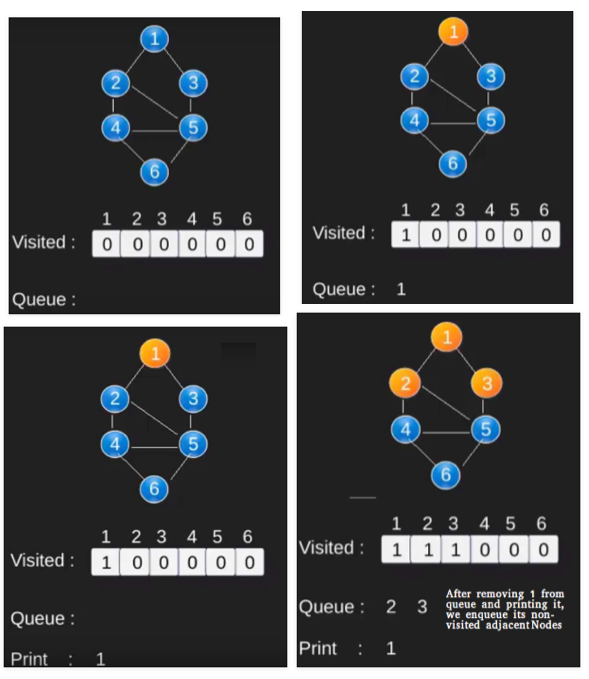
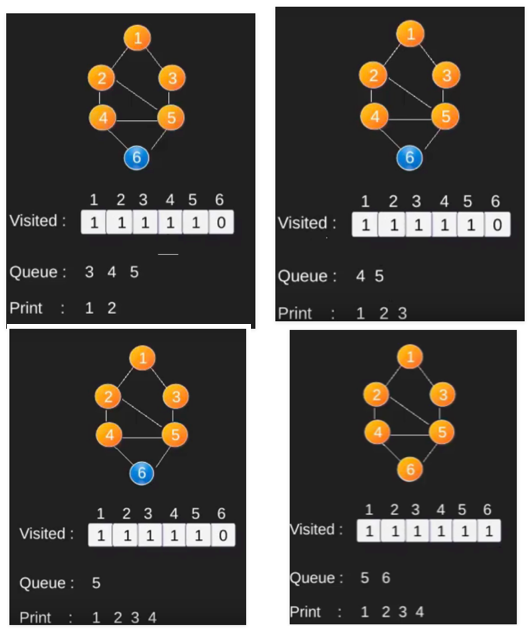
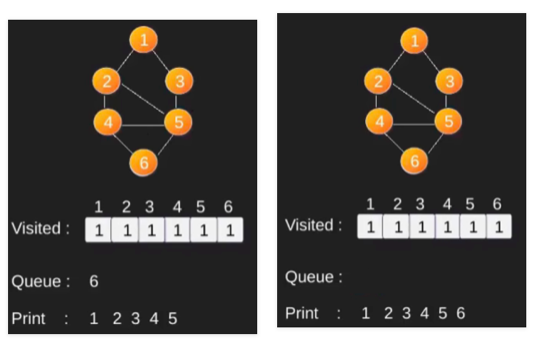
인접행렬
n, m, v = map(int, input().split())
matrix = [[0 for j in range(n+1)] for i in range(n+1)]
for _ in range(m):
a, b = map(int, input().split())
matrix[a][b] = 1
matrix[b][a] = 1
visit=[False]*(n+1)
def bfs(vertex_list):
global visit, matrix, n
if vertex_list:
tmp_list=[]
for i in vertex_list:
print(i, end=' ')
for j in range(n):
if matrix[i][j+1] and not visit[j+1]:
visit[j+1]=1
tmp_list.append(j+1)
bfs(tmp_list)
visit=[0]*(n+1)
visit[v]=1
bfs([v])
인접 리스트
#BFS
que = [s]
chk = set()
chk.add(s)
print(s,end=' ')
while que:
v = que.pop(0)
for u in sorted(adj[v]):
if u in chk : continue
print(u,end=' ')
que.append(u)
chk.add(u)
print()
참고자료: http://manducku.tistory.com/23?category=683258
https://www.geeksforgeeks.org/depth-first-search-or-dfs-for-a-graph/ [dfs 그림출처]
https://www.geeksforgeeks.org/breadth-first-search-or-bfs-for-a-graph/ [bfs 그림출처]
https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html
https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html