BST(binary search tree)란? 이진 트리가 BST인지 확인하는 법은?

10 Sep 2019

Reading time ~2 minutes

제 블로그의 모든 글은 IMHO로 쓴 것입니다. 잘못된 부분이 있으면 덧글을 통해서 소통을 하면 더 좋은 글로 발전이 될 수 있을 것 같습니다. 그렇지만 소통을 할 때 서로의 감정을 존중하는 선에서 해주셨으면 좋겠습니다. 감사합니다:) —

BST란?

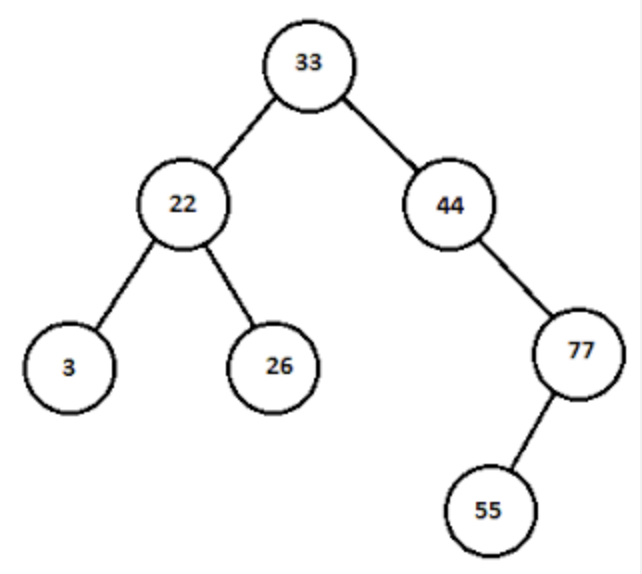
이진 검색 트리 (BST)는 다음과 같은 속성을 갖는 노드 기반 이진 트리 데이터 구조입니다.

노드의 왼쪽 하위 트리에는 키가 노드 키보다 작은 노드 만 포함됩니다.
노드의 오른쪽 하위 트리에는 키가 노드 키보다 큰 노드 만 포함됩니다.
왼쪽 및 오른쪽 하위 트리는 모두 이진 검색 트리 여야합니다.

비효율적 방법

각 노드에 대해 왼쪽 하위 트리의 최대 값이 노드보다 작고 오른쪽 하위 트리의 최소값이 노드보다 큰지 확인한다.

/* Returns true if a binary tree is a binary search tree */
int isBST(struct node* node){
  if (node == NULL)
  	return(true);

  /* false if the max of the left is > than us */
  if (node->left!=NULL && maxValue(node->left) > node->data)
  	return(false);

  /* false if the min of the right is <= than us */
  if (node->right!=NULL && minValue(node->right) < node->data)
  	return(false);

  /* false if, recursively, the left or right is not a BST */
  if (!isBST(node->left) || !isBST(node->right))
  	return(false);

  /* passing all that, it's a BST */
  return(true);
}

효과적인 METHOD :

위의 방법 2는 트리의 일부를 여러 번 통과하기 때문에 느리게 실행됩니다. 더 나은 솔루션은 각 노드를 한 번만 봅니다. 트릭은 유틸리티 도우미 함수 isBSTUtil (struct node * node, int min, int max)을 작성하여 각 노드를 한 번만 보면서 축소되는 최소값과 최대 허용 값을 추적하는 트리를 따라 이동합니다.

min 및 max의 초기 값은 INT_MIN 및 INT_MAX 여야합니다.

아래는 위의 접근 방식의 구현입니다.

import sys
INT_MAX = sys.maxsize
INT_MIN = -sys.maxsize-1

# A binary tree node
class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data  
        self.left = None
        self.right = None


# Returns true if the given tree is a binary search tree
# (efficient version)
def isBST(node):
    return (isBSTUtil(node, INT_MIN, INT_MAX))

# Retusn true if the given tree is a BST and its values
# >= min and <= max
def isBSTUtil(node, mini, maxi):

    # An empty tree is BST
    if node is None:
        return True

    # False if this node violates min/max constraint
    if node.data < mini or node.data > maxi:
        return False

    # Otherwise check the subtrees recursively
    # tightening the min or max constraint
    return (isBSTUtil(node.left, mini, node.data -1) and
          isBSTUtil(node.right, node.data+1, maxi))

# Driver program to test above function
root = Node(4)
root.left = Node(2)
root.right = Node(5)
root.left.left = Node(1)
root.left.right = Node(3)

if (isBST(root)):
    print "Is BST"
else:
    print "Not a BST"

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

출처:
https://www.geeksforgeeks.org/a-program-to-check-if-a-binary-tree-is-bst-or-not/

bst의 사진출처:

https://muckycode.blogspot.com/2015/01/binary-search-treebst.html