[DataStructure] binary_search_tree(이진탐색트리) by python3

07 Sep 2018

Reading time ~3 minutes

이진 트리란?

이진 트리 (binary tree)는 최대 두 개의 자식 노드를 가지는 트리 형태의 자료구조로서, 효율적인 탐색 혹은 정렬을 위해 주로 사용된다.
균형 트리의 시간복잡도는 삽입, 찾기, 삭제 모두 기본적으로 O(logn) 이다.
최악의 시간복잡도는 O(n) 인 데, 트리가 한쪽으로 치우쳐져 있을 때 원하는 것을 찾기 위해 전부 탐색을 해야 하기에 그렇다.

실제 코딩인터뷰를 할 때 최대한 O(logn) 의 시간복잡도 대답을 해야함으로, 자주 활용되는 dataStructure이다.

이진 탐색 트리란?

이진 탐색 트리 (binary search tree)는 이진 트리의 특수한 경우이다.
모든 노드에 대해 그 왼쪽 자식들의 값이 현재 노드 값보다 작거나 같으며, 그 오른쪽 자식들의 값이 현재 노드의 값보다 크다는 조건을 만족하면 이진 탐색 트리가 된다.

삽입

위의 그림대로 삽입 시 빈 노드를 찾아서, 옆으로 이동할 때 마다 계속 대소 비교를 한다.
처음 트리를 만들 때 루트 노드를 먼저 설정 된 채로 코드를 진행 되는 것으로 만들었다.

루트 노드를 먼저 삽입을 하는 코드

def __init__(self, data):
  self.data = data
  self.left = self.right = None

이후 삽입을 하는 코드

def insert(self, data):
  if data < self.data: # 대소 비교를 해서 어느 쪽 데이터를 탐색 할 것 인지 고른다.
    if self.left is None: # 없으면 거기에 새 노드를 생성한다.
      self.left = Node(data)
    else:
      # 이미 있을 때는 더 옆으로 움직이게 하기 위해서 self.left를 기준으로 다시한번 insert문을 돌린다.
      # 그러면 처음에는 root였지만 이제는 들어온 data를 기준으로 다시한번 insert문을 돌기 때문이다.
      # 즉 노드가 움직인다.
      self.left.insert(data)
  elif data > self.data:
    if self.right is None:
      self.right = Node(data)
    else:
      self.right.insert(data)

삭제

이진 트리의 좌우 균형이 맞으면 탐색/삽입/삭제의 시간복잡도가 O(logn)이다. 그러나 이진 탐색 트리는 정렬된 데이터에 취약하다. 오름차순이든 내림차순이든 정렬된 데이터가 입력되면 한쪽으로 치우친 (skewed) 트리가 만들어진다. 이 때, 최악의 경우 모든 데이터를 살펴야 할 수도 있어 시간복잡도가 O(n)이 된다.

def delete(self, data):
  if data == self.data:
    # data가 내가 지우고 싶은 data다.
    if self.left or self.right:
      if self.left.data :
          # 먼저 left를 선택하기 위해서 if문 앞쪽에 left 진위여부를 분기문에 놓는다.
        self.data = self.left.data
        # data 를 바꾸고
        # 그 자식들이 있으면 self.left에 놓는다.
        self.left = self.left.left or self.left.right
      elif self.rigth.data :
        self.data = self.right.data
        self.right = self.right.left or self.right.right
    else:
      # 자식이 없는 경우
      self.data = None
  elif data > self.data:
      self.right.delete(data)
  elif data < self.data:
      self.left.delete(data)

순회

우리가 잘 알고 있는 순회는 모두 깊이 우선 순회 방법(Depth First Traversal) 이다.
깊이 우선 순회에는 세가지 방법이 있다.

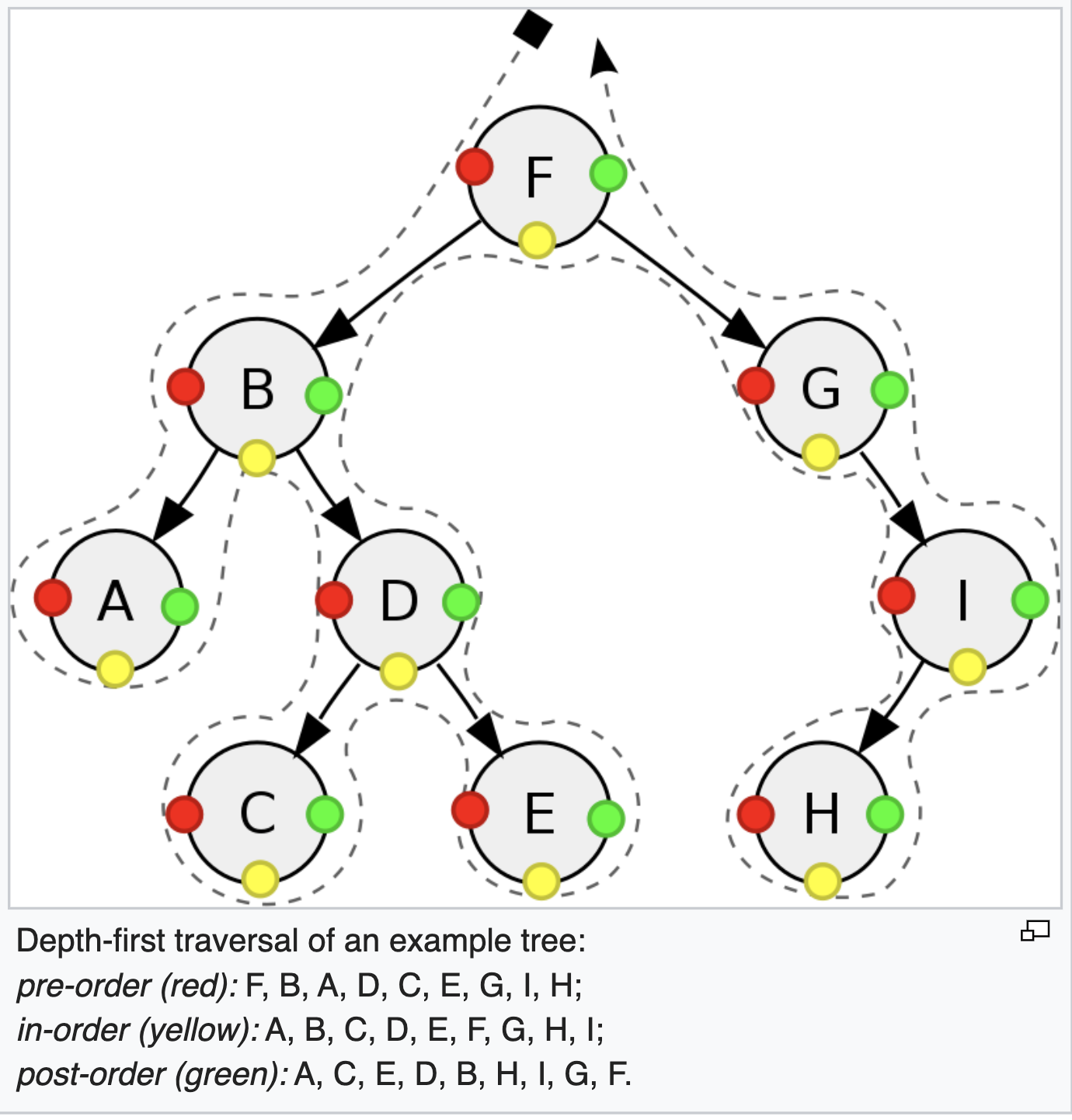
travelsal_tree

전위 순회(Pre-order traversal)
정위 순회(In-order traversal)
후위 순회(Post-order traversal)

어떤 노드들을 먼저 순회할 지에 따라 각 순회 방법을 나눈다. 그림으로 보면
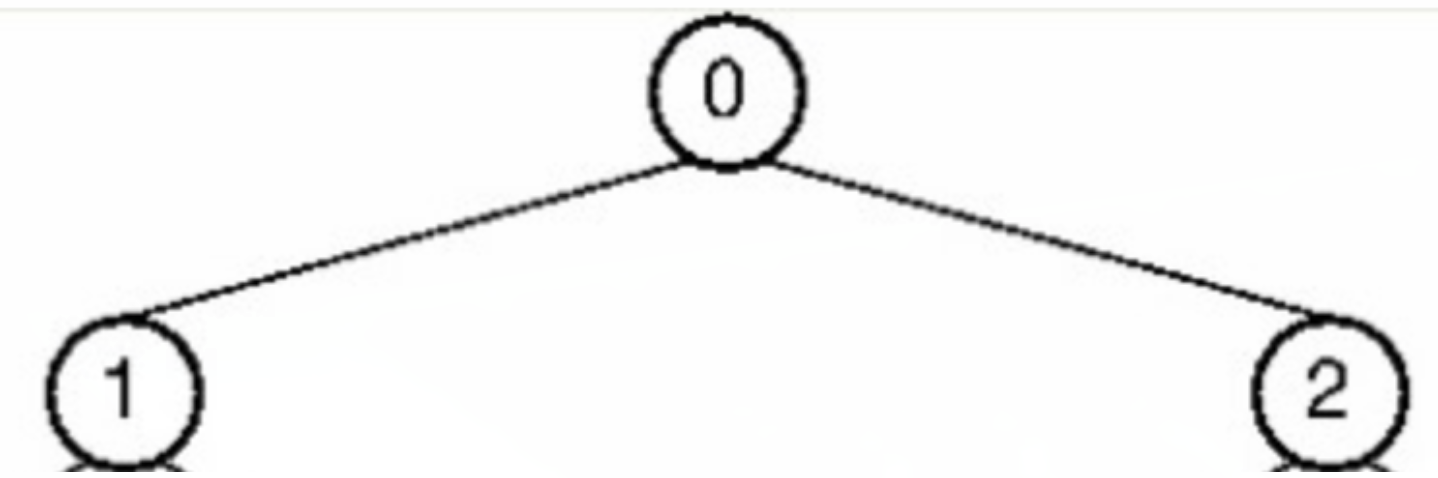travelsal 위와 같은 그림이 있을 때,

preorder: 0 1 2
inorder: 1 0 2
postorder: 1 2 0

Preorder traversal

Root -> Left ->Right
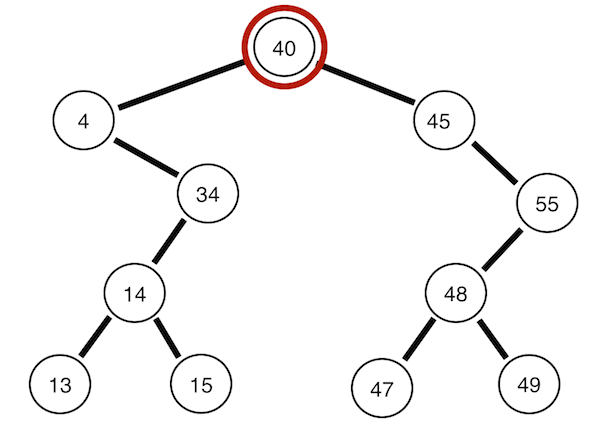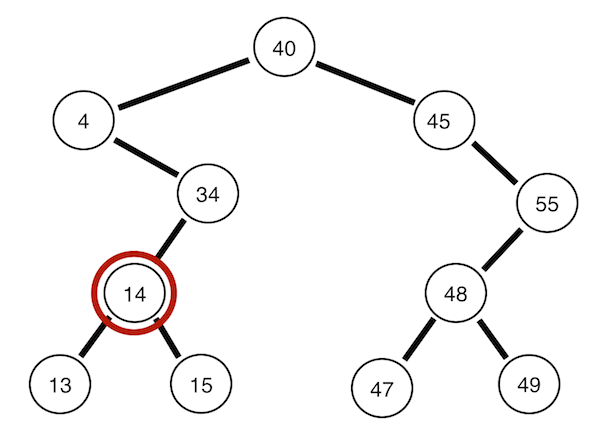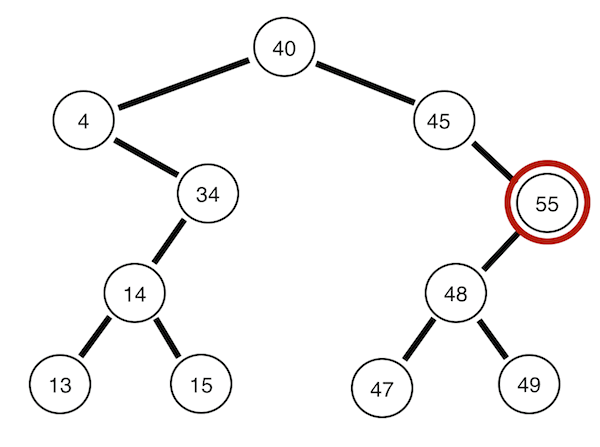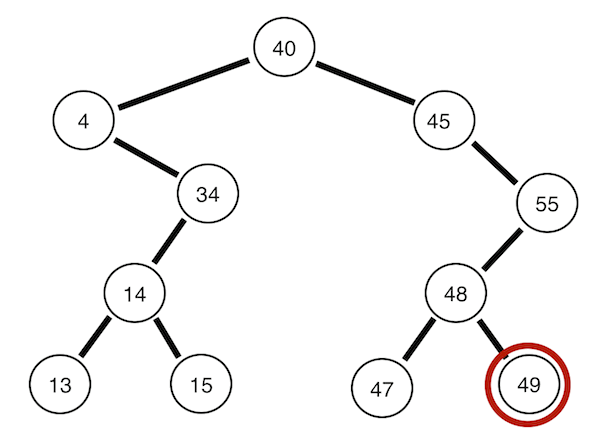
success

def PreorderTraversal(self, root):
  res = []
  if root:
    res.append(root.data)
    res += self.PreorderTraversal(root.left)
    res += self.PreorderTraversal(root.right)
  return res

Inorder traversal

Left -> Root -> Right
success

def InorderTraversal(self, root):
  res = []
  if root:
    res = self.inorderTraversal(root.left)
    # 왼쪽의 node가 없을 때 까지 계속 뒤로 내려가지 않고 호출된다.
    res.append(root.data)
    # root이다.
    res += self.inorderTraversal(root.right)
    # 오른쪽의 node가 없을 때 까지 계속 뒤로 내려가지 않고 호출된다.
  return res

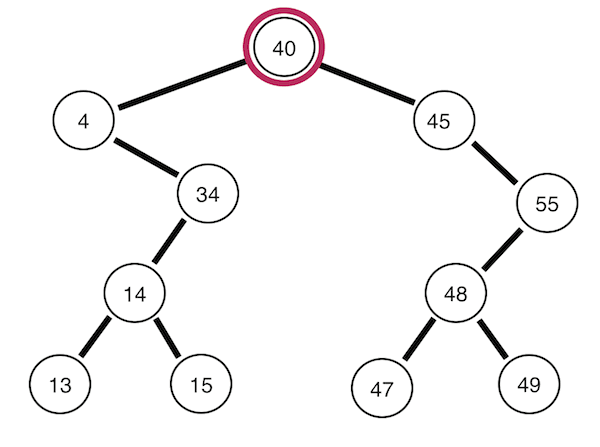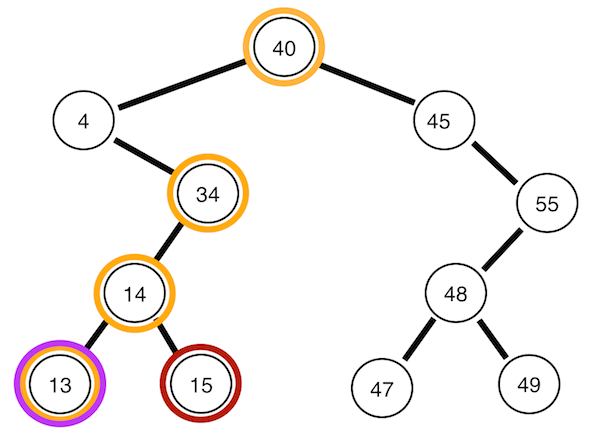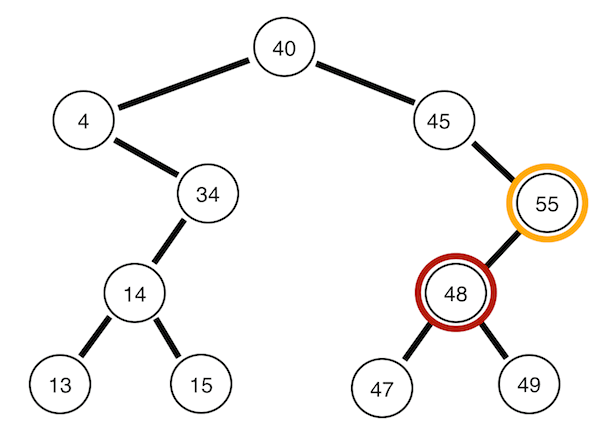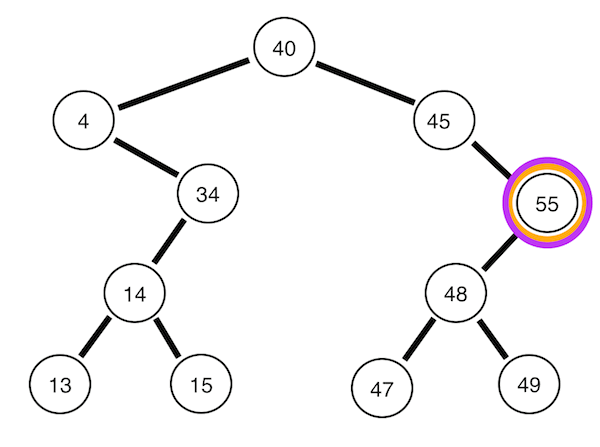
Postorder traversal

Left -> Right -> Root
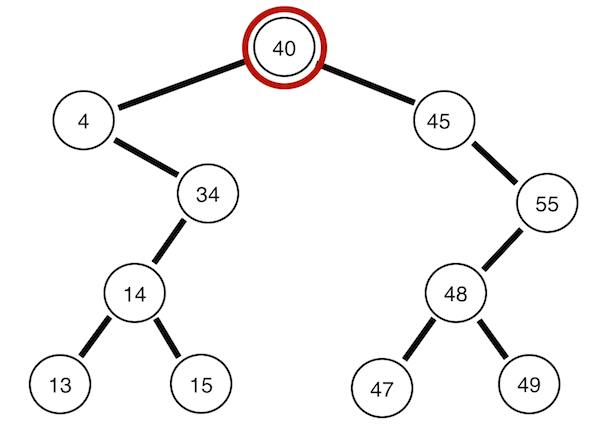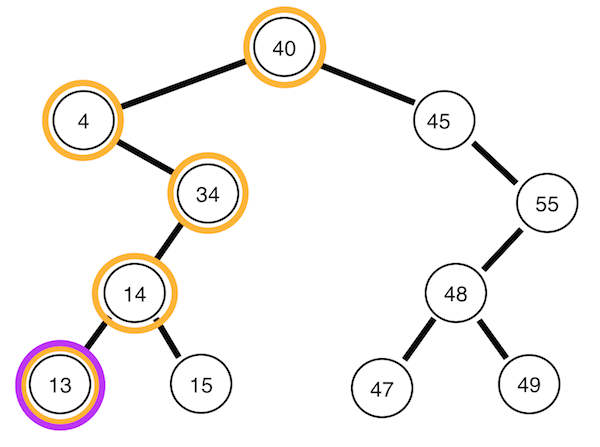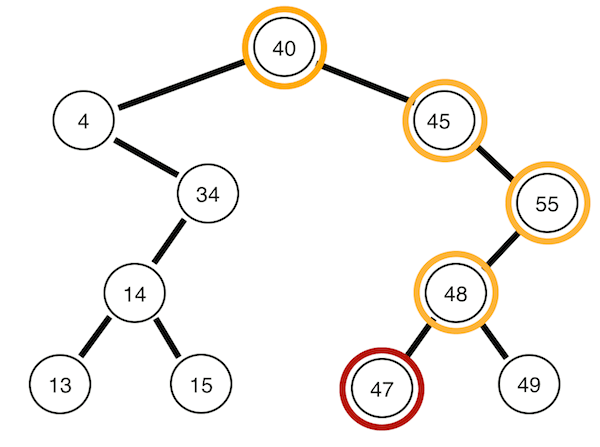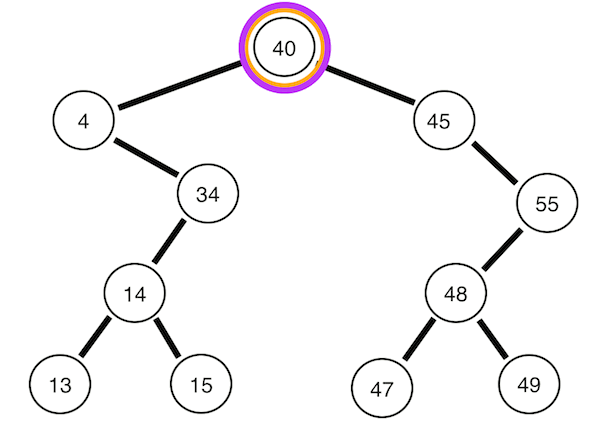
success

def PostorderTraversal(self, root):
  res = []
  if root:
    res = self.PostorderTraversal(root.left)
    res += self.PostorderTraversal(root.right)
    res.append(root.data)
  return res

총 코드

class Node:
  def __init__(self, data):
    self.data = data
    self.left = self.right = None

  def insert(self, data):
    if self.data:
      if data < self.data:
        if self.left is None:
          self.left = Node(data)
        else:
          self.left.insert(data)
      elif data > self.data:
        if self.right is None:
          self.right = Node(data)
        else:
          self.right.insert(data)
    else:
      self.data = data

  def delete(self, data):
    if data == self.data:
      if self.left or self.right:
        if self.left.data :
          self.data = self.left.data
          self.left = self.left.left or self.left.right
        elif self.rigth.data :
          self.data = self.right.data
          self.left = self.right.left or self.right.right
      else:
        self.data = None
    elif data > self.data:
        self.right.delete(data)
    elif data < self.data:
        self.left.delete(data)

  def InorderTraversal(self, root):
    res = []
    if root:
      res = self.InorderTraversal(root.left)
      res.append(root.data)
      res = res + self.InorderTraversal(root.right)
    return res

  def PreorderTraversal(self, root):
    res = []
    if root:
      res.append(root.data)
      res = res + self.PreorderTraversal(root.left)
      res = res + self.PreorderTraversal(root.right)
    return res

  def PostorderTraversal(self, root):
    res = []
    if root:
      res = self.PostorderTraversal(root.left)
      res = res + self.PostorderTraversal(root.right)
      res.append(root.data)
    return res

root = Node(21)
root.insert(28)
root.insert(14)
root.insert(32)
root.insert(25)
root.insert(18)
root.insert(11)
root.insert(30)
root.insert(19)
root.insert(15)
print(root.InorderTraversal(root))
print(root.PreorderTraversal(root))
print(root.PostorderTraversal(root))
# 이분탐색 때 -1하는 이유는 노드 삽입시 계속 옆으로 가서 비교를 하는 것 과 같은 것이다.

참고 자료:
http://ejklike.github.io/2018/01/09/traversing-a-binary-tree-1.html#fnref:1
https://wkdtjsgur100.github.io/order-summary/