[백준] 9095번 : 1, 2, 3 더하기 with python, java

22 Aug 2018

Reading time ~1 minute

문제 : https://www.acmicpc.net/problem/9095

목표:

n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 수 출력

조건:

합을 나타낼 때는 수는 한개여도 상관없다.
- 4
  - 1+1+1+1
위치가 다르면 들어간 숫자가 같아도 다른 경우의 수다.
- 4 (모두 다른 경우의 수)
  - 1+1+2
  - 1+2+1
  - 2+1+1

solution 설명 :

O(N)
dp를 사용
dd의 index는 i를 구성하는 경우의 수다.

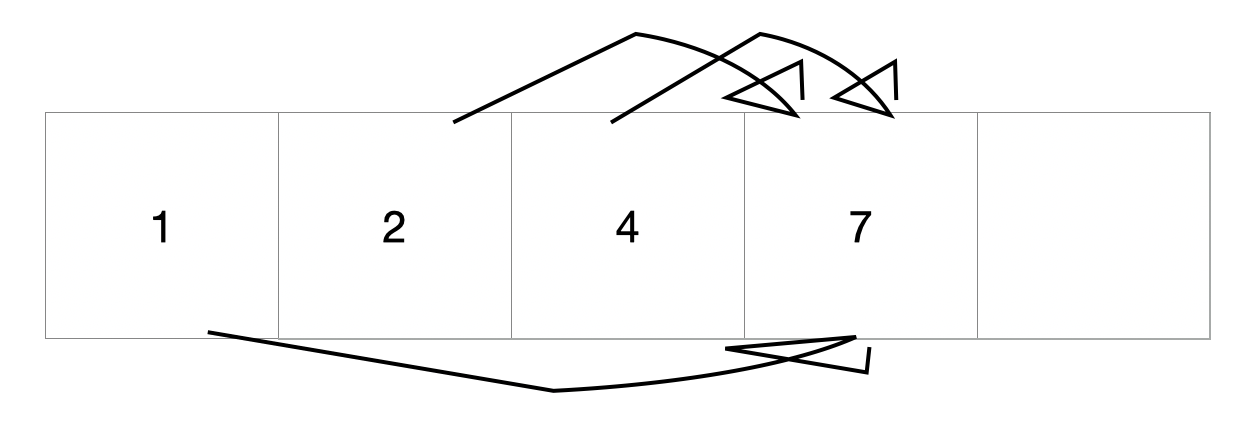
description

dd[4] 경우 -  dd[1]에서 +3을 해 dd[4]를 이룬다. 
- dd[2]에서 +2를 해 dd[4]를 이룬다. 
- dd[3]에서 +1를 해 dd[4]를 이룬다. 
- 그렇기 때문에 dd[4] = dd[1] + dd[2] + dd[3] 이다.
dd[i]에는 dd[i-1], dd[i-2], dd[i-3]의 경우의 수를 더한 값을 넣는다.

def solved(n):
    dd = [1, 2, 4]
    for i in range(3,n):
        dd += [dd[i-3] + dd[i-2] + dd[i-1]]
    return dd[n-1]

for _ in range(int(input())):
    print(solved(int(input())))

import java.util.*;
import java.math.*;

public class Main {
    public static void main(String args[]) {
        Scanner sc = new Scanner(System.in);
        int[] d = new int[11];
        d[0] = 1;
        for (int i=1; i<=10; i++) {
            for (int j=1; j<=3; j++) {
                if (i-j >= 0) {
                    d[i] += d[i-j];
                }
            }
        }
        int t = sc.nextInt();
        while (t-- > 0) {
            int n = sc.nextInt();
            System.out.println(d[n]);
        }
    }
}

algorithm 백준