2019_Round_A Training solution

21 Mar 2020

Reading time ~1 minute

문제 링크 : 2019_Round_A_1_Training

문제 설명

N명 중 skill rate가 같은 P명을 선발
한시간당 한명만 점수를 높일 수 있다.
선발시간은 최소 시간을 구한다.

즉

N= 4, P=3
3 1 9 100

일 경우

3 1 9

를 뽑아서

9 9 9

3->9 로 만드는데 6시간 1->9 로 만드는데 8시간

14이 답이다.

조건

Limits
- Time: 15 seconds per test set.
- Memory limit: 1 GB.
- 1 ≤ T ≤ 100.
- 1 ≤ Si ≤ 10000, for all i.
- 2 ≤ P ≤ N.
Test set 1 (Visible)
2 ≤ N ≤ 1000.
Test set 2 (Hidden)
2 ≤ N ≤ 10**5. O(N)이나 O(NlogN)

풀이

정렬 후 구간합(Sum of Interval)사용

N= 4, P=3

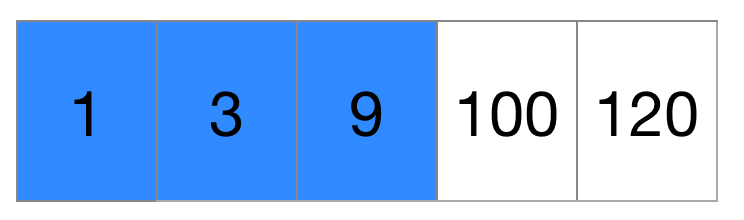
=> 9(기준시간) * 2 - (1 + 3) = 14

=> 100(기준시간) * 2 - (3 + 9) = 188

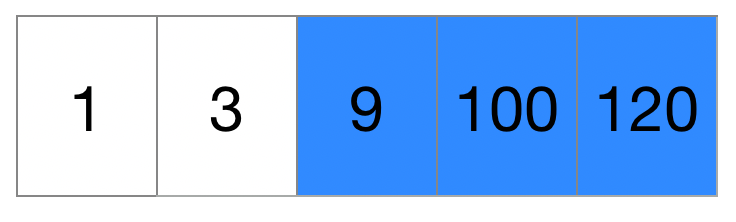
=> 120(기준시간) * 2 - (9 + 100) = 131

정렬한 이유는 이곳에서는 더하기만 되고 선수들의 위치는 바꿀 수 있다.
기준을 세워서 차의 합을 만들면 optimize가 된다.

import sys

def solved(N, P):
    SR = list(map(int, input().split()))
    SR.sort()

    # 첫번째 총합
    sum = 0
    for i in range(P-1):
        sum += SR[i]
    ans = SR[P-1] * (P-1) - sum

    for i in range(P,N):
        sum = sum - SR[i-P] + SR[i-1] # 각 구간별 총합을 구하는 식
        total = SR[i] * (P-1) # 총 팀원의 실력 합
        ans = min(ans, total-sum)

    return ans

for t in range(1, int(input())+1):
    N, P = map(int, input().split())
    print("Case #{}: {} ".format(t, solved(N, P)))